

QUEST
Wave-like behaviour
In this entry you will find information about what quantum wave-like behaviour is. Begin from the approach that feels easier or closer to you (play, discover, or learn), and then explore the others and see how your understanding of wave-like behaviour shifts and expands!
Play
This is a puzzle game which explores wave-like behaviour of particles. This game can be played by one or two players, who have to reach the exit and avoid enemies by interacting with light and electrons.
Credits:
Aditya Anupam
Advisors/collaborators: Dr. Nassim Parvin, Professor Azad Naeemi
http://learnqm.gatech.edu/
contact: aanupam3@gatech.edu
In this video, the authors of the game introduce themselves and explain the physics behind their game and how to play it.
Discover
Prof. Maria Luisa Chiofalo is a quantum physicist at the University of Pisa (Italy) specialised in condensed matter physics and quantum fluids, and with an interest in quantum biology.
In this video, she explains the wave-like behavior in the context of quantum physics.
In the quantum state entry, we introduce the notion of the vectorial sum of spin states in the framework of Stern-Gerlach (SG) experiments. This mathematical formalisation gains a deeper meaning when discussing superposition and the Heisenberg uncertainty principle: given that measuring the spin in, say, the horizontal direction erases all previous information regarding the vertical spin component, we express this uncertainty in terms of a superposition of vertical components. However, we also mention there that such superposition does not mean “the spin is in the $| \uparrow \rangle$ or $| \downarrow \rangle$ state, and we don’t know which” but, instead, it is more appropriate to state something along the lines “it is in the $| \uparrow \rangle$ and $| \downarrow \rangle$ states at the same time”. What leads us to assert something like that? In short, the answer is that we observe phenomena that are inconsistent with the first reading, but can be explained by considering that the atom behaves as if it were in both states simultaneously, and those two behaviours could inferfer with one another. This mind-bending phenomenon, quantum interference, is often referred to as wave-like behaviour. In this entry, we will introduce a version of the SG experiment in which this will become apparent.
Before we do that, however, let us introduce a small modification of the Stern-Gerlach apparatus, depicted in Figure 1 below. Essentially, we have added some extra magnets that counteract the first one, so that a spin (for example, a silver atom) deviated from the initial central trajectory in the direction of the magnetic field (e.g., upwards or downwards if it's vertically oriented) can return to it. Later on, we will also add an obstacle blocking one of the two paths, for instance, the bottom one. In that case, the beam deviating in such direction is stopped by the obstacle, while the beam deviated in the opposite direction can continue its path and leave the apparatus. You should take a moment to convince yourself that this is equivalent to the original SG apparatus introduced in the quantum state entry: leaving the vertically oriented apparatus corresponds to an impact on the upper side of the plate in the original set-up (up-directed beam), while not leaving the apparatus corresponds to an impact on the bottom side of the plate (down-directed beam). Keep in mind that, in the absence of the block, both beams return to the original central trajectory.
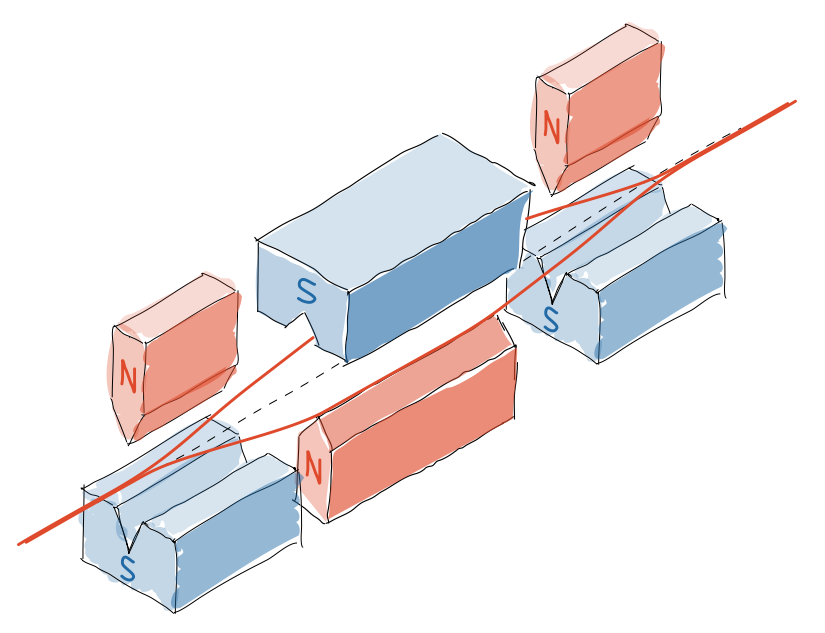
Fig 1: In this modified SG apparatus, a beam deflected upwards or downwards by the first magnet is driven back to its original incoming trajectory by the other magnets. Hence, blocking one of the two possible trajectories allows us to measure the spin, as only the atoms that deviate in the opposite direction can leave the device.
Let us now revisit the sequence of SGs with a similar setting to the one considered in the superposition entry, this time using the new version of the apparatus in the second one (that is, the SG$\hat{\mathbf{x}}$ is now the device from Figure 1 with the magnet horizontally oriented, i.e., rotated 90 degrees, and with an obstacle on the left-deviated path). Moreover, we also block the last $S_z$+ output channel, as depicted in Figure 2. Initially, a beam of spins coming from the oven enters the first of them and, as we now know, the ones conforming the upper outgoing beam are in the $| \uparrow \rangle$ state. Right after, they enter the second apparatus, which selects those deflecting to the right, so the outgoing beam is made out of spins in the $| \rightarrow \rangle$ state. Finally, they go into the third Stern-Gerlach apparatus.
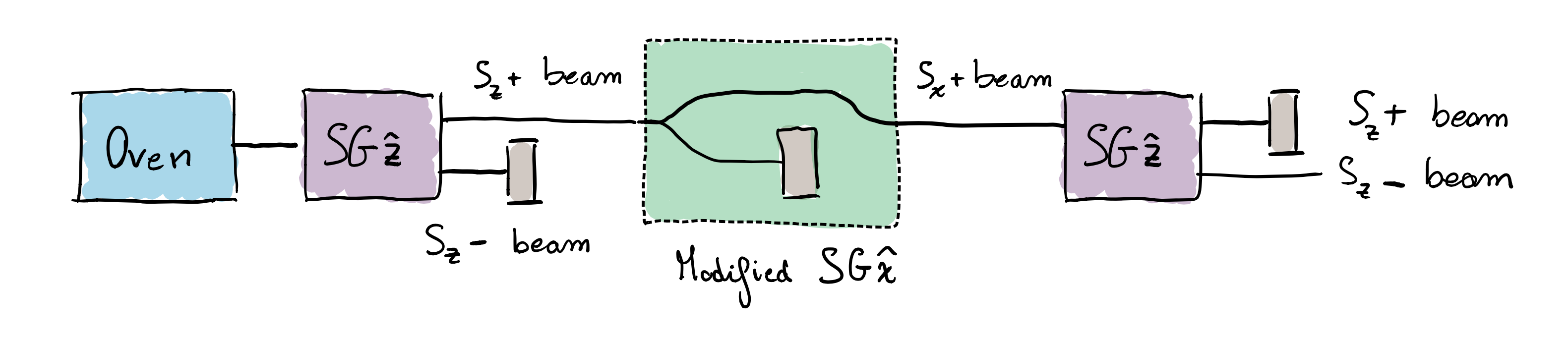
Fig 2: Sequence of SG apparatus in different directions, as indicated by the labels. The central apparatus (in green) is the modified version oriented in the horizontal $x$-direction. The $S_x$- beam (bottom in the figure) collides with the obstacle, while the other beam leaves the apparatus. When removing the obstacle, both beams exit together in the same direction.
As we explain in the superposition entry, some atoms still make it outside this last device, that is, the beam directed downwards appears once again, despite having been measured in the “up” state earlier. This is a manifestation of the Heisenberg uncertainty principle. Up to this point, this is very similar to what we discuss in those entries, but let us now add a plot twist. Suppose that we remove the block in the second apparatus, that is, the obstacle in which all the spins deviating towards the left get stuck. What happens now to the beam leaving the third apparatus (that is, the last $S_z$- beam that avoids the last obstacle)? Let us analyse the situation. Classically, one would expect that, in the second apparatus, the spins deviate either left or right and then all of them return back to the original trajectory (because there’s no obstacle on either path), either in the state $| \leftarrow \rangle$ or $| \rightarrow \rangle$, even if we don’t know which. Hence, the whole beam should leave the second apparatus with a well-defined horizontal spin component. Given that a beam with well-defined horizontal spin component splits in a vertical SG apparatus (see the superposition entry), we would expect to observe a beam leaving the third one too. What is more, since we have removed an obstacle that was stopping many of the atoms, there should be more making it to the very end of the experiment. As reasonable as this hypothesis may seem, it is wrong. And as unreasonable as it may seem, the right answer is that not a single spin leaves the third apparatus! A little rephrasing may help evidencing how extraordinary this result is: removing an obstacle in the trajectory of the spins, which was effectively stopping them, makes it impossible for any of them to go through, while blocking one of the possible paths allows them to pass. Were it not because this is confirmed by experiments, we would immediately deem this as nonsense and move on. Instead, it turns out this is how Nature actually behaves.
How can we understand or interpret such strange phenomenon? The first thing to notice is that, given that in the absence of the second obstacle all the spins deviate upwards in the third SG, the second apparatus has no effect on the state of the spins whatsoever. Indeed, recall from the superposition entry that the beams that do not deflect downwards at all are those that previously left a SG apparatus in the upwards direction (and for which nothing else happened in between). Nevertheless, the second apparatus, albeit without the obstacle, is there, so it must deflect the trajectories of the spins; in fact, we see this happening when we add the obstacle blocking any of the two horizontally deviated paths and part of the beam is stopped. Moreover, if we only let one of the two horizontally deviated beams go through, a beam deviated downwards emerges. After this considerations, the question becomes: how can we put these observations together? QM provides a beautifully simple answer, perhaps not aimed at fulfilling philosophical urges, but one furnished with the solid logical consistency and quantitative power of mathematics. According to the superposition principle, the state of the spin can be written in terms of a superposition (a sum) of other states. In particular, for the spins leaving the first SG apparatus in the $| \uparrow \rangle$ state we have $| \uparrow \rangle = ( | \leftarrow \rangle + | \rightarrow \rangle ) / \sqrt{2}$, which can only be given a vague in-words interpretation such as “in the absence of the obstacle, spins go through both horizontally deviated paths, left and right, and interfere with themselves, yielding spins with a well-defined vertical spin component''.
This is an example of the so-called quantum interference phenomenon. The well-known wave-like behaviour of quantum particles is analogous: a particle allowed to pass through two slits (without physically revealing any information of which path it chooses) passes through both and interferes with itself, as observed in the celebrated double-slit experiment. When we repeat such experiment many times, allowing only one particle to pass at a time, we observe a collection of point-like impacts on a photographic plate to which the particles arrive after passing through the double slit. The density of these point-like collisions forms an interference pattern mathematically consistent with that of a wave.
We reiterate at this point that, however strange the explanation and formalisation presented here may seem, the experimental results do not lend themselves to any known simpler explanation. Moreover, QM has proven its predictive power in numerous — and often times even more convoluted — situations.
Learn
In this link you will find the proper definition of the wave-function and a clarification on the meaning of the so-called wave-particle duality.
Contact
Social
Menu
© QPlayLearn 2020 | Design by Bitflow