

QUEST
Superposition
In this entry you will find information about what quantum superposition is. Begin from the approach that feels easier or closer to you (play, discover, or learn), and then explore the others and see how your understanding of superposition shifts and expands!
Play
Quantum TiqTaqToe is a quantum version of regular Tic Tac Toe. The game familiarizes you with quantum superposition by allowing you to place quantum moves. A higher level of quantumness introduces entanglement as an additional quantum move available to the player.
Credits:
Evert van Nieuwenburg
https://quantumtictactoe.com/
contacts: evert.v.nieuwenburg@gmail.com
In this video, the author of the game introduces himself and explains the physics behind his game and how to play it.
Discover
Dr. Lorenzo Maccone is an associate professor at the Quantum Information Theory Group in Pavia University (Italy), working on quantum information and foundations of quantum mechanics.
In this video, he presents the concept of superposition using shapes and colors.
To explain the concept of quantum superposition, we will make use of the Stern-Gerlach (SG) experimental framework, which we describe in the entry of quantum state. If you haven’t read it yet, we recommend you to pay a visit to its Discover part. We will now consider sequential SG experiments, where the atomic beams go through two or more SG apparatus in sequence.
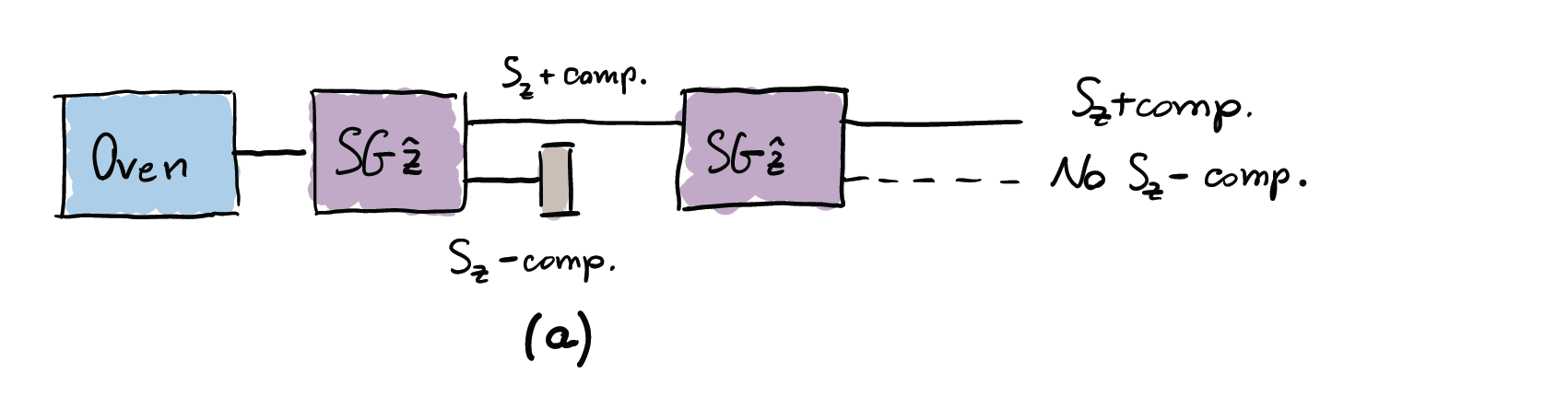
Let us begin by adding a second SG identical to the first one, as depicted in picture (a). We use the notation SG$\hat{\mathbf{z}}$ to identify a SG apparatus with the magnetic field oriented vertically ($z$-axis). As we know, at the exit of the first SG, the beam is split into two parts, one directed downwards and another one directed upwards, each corresponding to one of the two possible values $\pm\hbar/2$ of the vertical component of the spin. We block the downwards-directed component, the $S_z$-, and let the remaining upward part, $S_z$+, be subjected to another SG$\hat{\mathbf{z}}$ apparatus. This time, we will find only one beam coming out of the second apparatus: all the atoms will be deflected upwards again. This means that the only possible outcome is the $S_z$+ component. This is perhaps not so surprising: if all the atom spins are up, we expect that they remain so if nothing happens between the first and the second SG$\hat{\mathbf{z}}$ apparatus.
Let us now play a bit with the spins, and see what happens if we start to add SG apparatus oriented in other directions. For instance, this time, after the first SG$\hat{\mathbf{z}}$, we add a second apparatus along the path of the up component only, but with the magnetic field along the horizontal direction, parallel to the $x$-axis. We identify it with the symbol SG$\hat{\mathbf{x}}$. Such arrangement is depicted in picture (b):
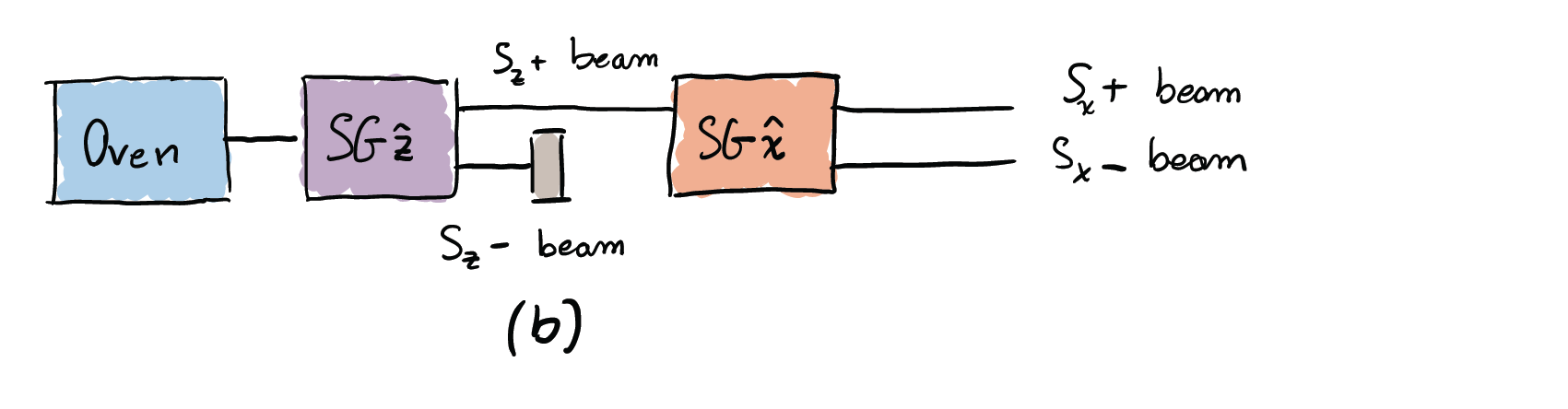
What would one expect following a classical line of reasoning? One might assume that, given that the magnetic moments of the atoms leaving the first SG apparatus are vertically oriented, they would not be deflected by a magnetic field in a perpendicular direction, and would hence not be affected by the SG$\hat{\mathbf{x}}$ apparatus. In the experiment, however, not only the atomic beam is deflected, but it is also split in two beams again, so that only two outcomes “left” ($S_x$-) or “right” ($S_x$+), are registered on the plate with equal intensities. One could still hypothesise that the upward beam, with $S_z=+\hbar/2$, entering the second apparatus (SG$\hat{\mathbf{x}}$), is composed of atoms that also have a well-defined x-component that is $S_x=+\hbar/2$ for half of them, and $S_x=-\hbar/2$ for the other half. In other words, the spins leaving the second apparatus would have well-defined $z$- and $x$-components, given that both have been measured.
In order to assess experimentally whether this is true, let us add a third apparatus to the scheme illustrated in picture (b). In particular, we include another SG$\hat{\mathbf{z}}$ apparatus along the path of the right-directed beam, i.e., for the spins with $S_x=+\hbar/2$, identified by $S_x$+. Such arrangement is depicted in picture (c):
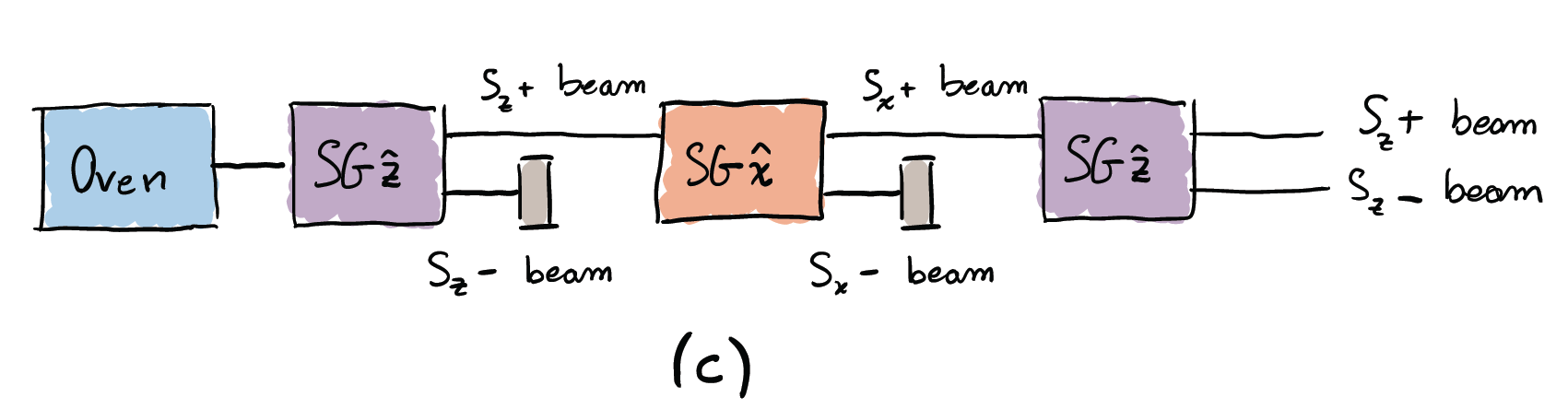
Since the third apparatus is identical to the first one, if the classical hypothesis were correct, all the atoms that deviated upwards in the first SG should be again deflected upwards by the third vertical magnet. Therefore, the atomic beam should be deflected, but not split. However, the experiment shows that two components emerge from the third apparatus instead of one. What we observe dispels any doubt that the classical hypothesis is inconsistent with the experimental results.
This clearly shows that the two components $x$ and $z$ of the spin cannot both be determined at the same time and indeed this is a manifestation of the Heisenberg uncertainty principle, which is described in related Discover entry of Quest. One can think, following classical lines, that when one measures one of the two components, say $x$, the other one, say $z$, becomes randomly modified so that it is well-defined but acquires a value which we do not know due to the heavy disturbance of the last measurement. However, this is also inconsistent with another observation, namely, the quantum interference or wave-like behaviour. What this means is that rather than the $z$ component being well-defined but unknown to us, one can devise an experiment whose results are consistent with the assumption that both states “up” and “down” exist at the same time! Mathematically, this is incorporated in the superposition principle, which states that the vector describing the state of the system can be decomposed as the sum of vectors describing other quantum states. In the case of the example above, the state is written as
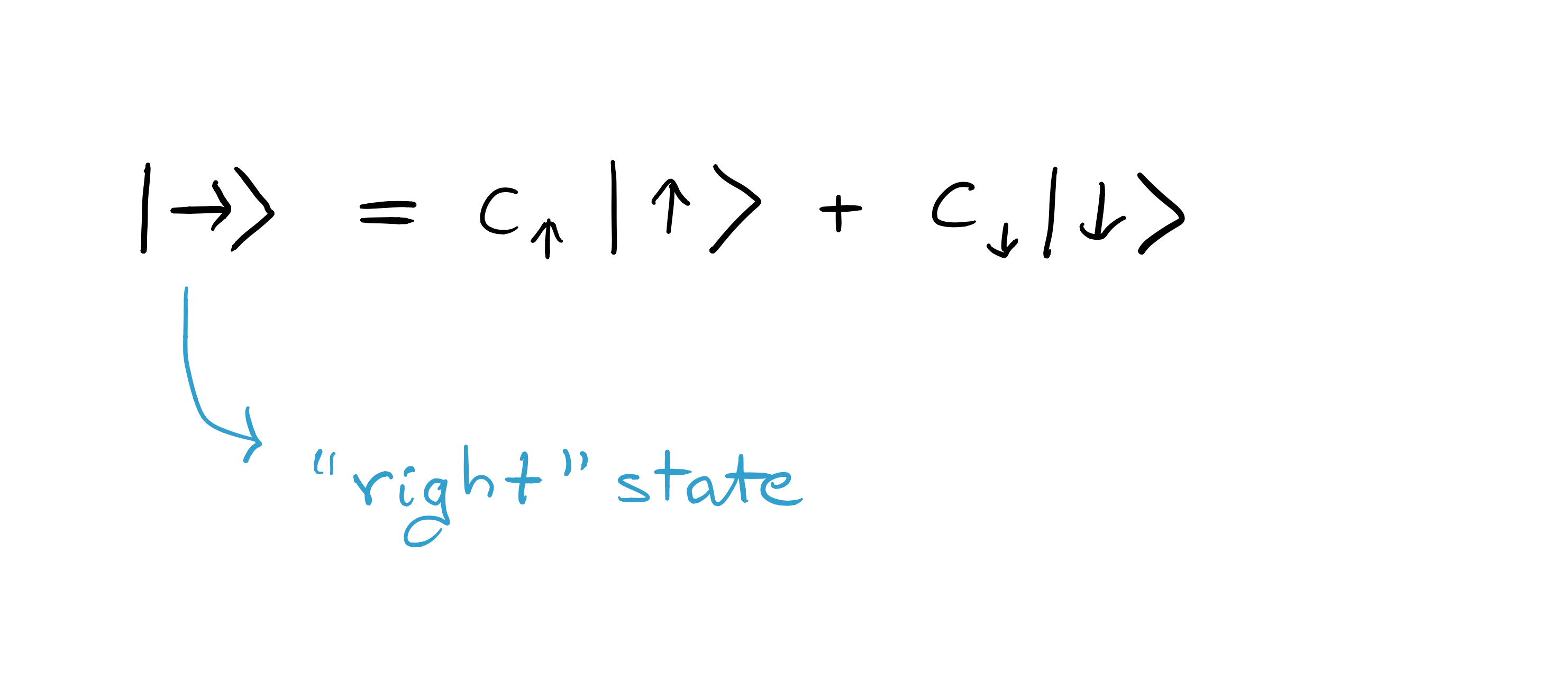
A little rephrasing may help to understand things a bit better: the main point is that after leaving the second apparatus in picture (c), the “right” state $|\rightarrow\rangle$, with $S_x=+\hbar/2$, should not be considered as merely being either in state “up” or “down”, but rather in “up” and “down”. Loosely speaking, we may say that the spin is “in both states at the same time” (although such a sentence seems quite meaningless unless it is understood as a verbalisation of a precise mathematical statement).
Learn
In this link you’ll find a short mathematical description of quantum superposition in terms of sums of vectors in Hilbert spaces. As an example, we show superposition of electron spins.
Contact
Social
Menu
© QPlayLearn 2020 | Design by Bitflow