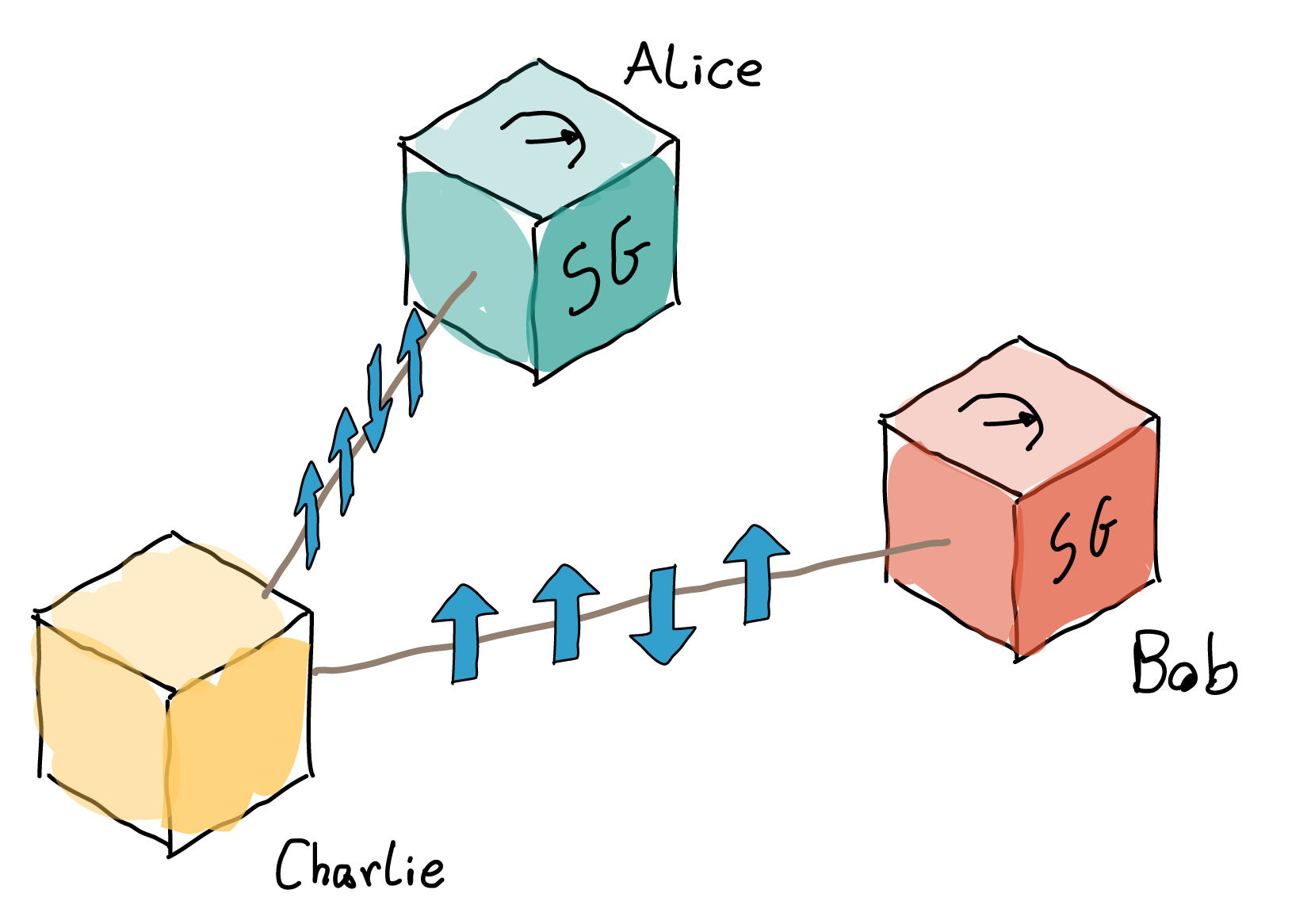
We consider three parties, Alice, Bob, and Charlie, who will be preparing and measuring pairs of spins. Specifically, we will assume that Charlie has access to a large source of spins, as well as the knowledge and experimental devices necessary to prepare them in any state he wants (as long as it is physically possible). Charlie will thus prepare pairs of spins in some state, and send one of the spins to Alice and the other one to Bob. Alice and Bob will then measure their respective spins using a Stern-Gerlach apparatus (see Quest entry on
quantum state) oriented along some direction, which they can agree upon, and compare the outcomes. Charlie is faced with the task of correlating such outcomes: both Alice and Bob should obtain random outcomes in the direction they choose, but the random outcomes should match each other's.
Charlie's first strategy involves a coin. He decides to toss one and, if the outcome is ``heads'', to prepare two spins in the state $|\uparrow\rangle$. If the outcome is “tails”, he prepares them in the state $|\downarrow \rangle$. The two spins are then sent to Alice and Bob (one each), who measure them in the vertical direction. As described in the Quest entry on
measurement, if Alice and Bob receive their spins in the state $|\uparrow \rangle$, they will both observe outcome “up”, while it will be “down” if Charlie got “tails” in the coin toss. After repeating the process many times, that is, after Charlie has sent many pairs of spins prepared in this way, Alice and Bob meet and compare the outcomes. They conclude that, while they individually obtained “up” or “down” randomly with probability $p = 1/2$, their outcomes were perfectly correlated.
They now decide to repeat the process with a slight difference: Charlie will continue to prepare the pairs in the both $|\uparrow\rangle$ or both $|\downarrow\rangle$ states randomly, but Alice and Bob will measure the horizontal spin component $x$ instead. What will the probabilities for Alice and Bob to observe “left” or “right” be? Will the outcomes be correlated in this case? Try to guess the answer before reading it (Hint: check the Quest entry on
measurement). Let us analyse the situation. Suppose Charlie obtained “heads” and hence prepared two spins in the $|\uparrow\rangle$ state. Alice thus receives a spin in the $|\uparrow\rangle$ state and measures it in the horizontal direction. This yields “left" or “right” with probability $p = 1/2$. The situation is identical for Bob. But should they necessarily observe the same outcome (both “left" or both “right”)? Well, for all we know, these two spins have been prepared in the $|\uparrow \rangle$ state independently, so we can consider them as two different spins coming out of a vertically oriented Stern-Gerlach apparatus, so they can yield different results when measured in the horizontal direction. Therefore, there is no reason to expect their outcomes to be correlated at all. Half of the times that Alice obtains “left", Bob obtains “right”; the other half, he obtains “left” (idem when Alice obtains “right”).
As long as Charlie prepares pairs of spins in this way, that is, conferring each of them a well-defined spin component along some direction, perfect correlations in the outcomes will be limited to those specific directions. Indeed, as a consequence of the
Heisenberg principle (see related Quest entry), the spin component in a direction perpendicular to the perfectly well-defined one is completely undetermined, which means that its measurement yields a completely random outcome, uncorrelated with anything else. But this is not everything Charlie can do. Instead, he can correlate the spins “the quantum way”, that is, entangling them.
According to QM, the Hilbert space of a system composed of two parts is the tensor product of their individual Hilbert spaces. In practice, this means the following. If a spin $A$ can be in some arbitrary superposition of $|\uparrow\rangle_A$ and $|\downarrow\rangle_A$ states, and another spin $B$ can also be in an arbitrary superposition of $|\uparrow\rangle_B$ and $|\downarrow\rangle_B$ states, they can jointly be in an arbitrary superposition of states $|\uparrow\rangle_A \otimes |\uparrow\rangle_B$, $|\uparrow\rangle_A \otimes |\downarrow\rangle_B$, $|\downarrow\rangle_A \otimes |\uparrow\rangle_B$, and $|\downarrow\rangle_A \otimes |\downarrow\rangle_B$, where the circled product symbol, $\otimes$, represents the tensor product; the mathematical properties of this product need not be introduced here. For our current purposes, we can read it as a mathematical version of “and”. For example, the state $|\uparrow\rangle_A \otimes |\downarrow\rangle_B$ can be read as “spin $A$ in the $|\uparrow\rangle_A$ state and spin $B$ in the $|\downarrow\rangle_B$ state”. To see how this works, let us revisit the previously discussed situation in which Charlie prepares the two spins in the $|\uparrow\rangle$ state and Alice and Bob measure in the horizontal direction. From the Quest entry on
wave-like behaviour, we know that $|\uparrow\rangle = ( |\leftarrow\rangle + |\rightarrow\rangle ) / \sqrt{2}$, hence we can write the following
$$
|\uparrow\rangle_A \otimes |\uparrow\rangle_B = \frac{1}{\sqrt{2}} \left(|\leftarrow\rangle_A +|\rightarrow\rangle_A \right) \otimes \frac{1}{\sqrt{2}} \left( |\leftarrow\rangle_B + |\rightarrow\rangle_B \right).
$$
To work out this expression, we need to use the associative property of the tensor product (which works just like in the regular product of numbers), resulting in
$$
\begin{aligned}
|\uparrow\rangle_A \otimes |\uparrow\rangle_B =&
\frac{1}{2} |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B + \frac{1}{2} |\leftarrow\rangle_A \otimes |\rightarrow\rangle_B \\
&+ \frac{1}{2} |\rightarrow\rangle_A \otimes |\leftarrow\rangle_B + \frac{1}{2} |\rightarrow\rangle_A \otimes |\rightarrow\rangle_B.
\end{aligned}
$$
In words, the joint state is in a superposition of all possible combinations of well-defined horizontal spin components. According to the third postulate of QP, see Quest entry on
quantum physics, Alice and Bob will measure any of these outcomes with probability $p = | 1/2 |^2 = 1/4$, just as explained earlier in non-mathematical terms.
Now, notice that the superposition in the last expression was obtained by expanding the terms in a tensor product of two single-spin states, $|\uparrow\rangle_A$ and $|\uparrow\rangle_B$. However, not all the superpositions of two-spin states are of this form. For example, consider the state $|\Psi\rangle_{AB} = (|\uparrow\rangle_A \otimes |\uparrow\rangle_B +|\downarrow\rangle_A \otimes |\downarrow\rangle_B) / \sqrt{2}$. This state is not a tensor product of single-spin states. Try to prove it yourself! We call the states that are not separable in terms of single-spin states entangled. But this notion seems rather mathematical, in the sense that we are referring to a property of the mathematical description of the state, rather than to a physical phenomenon. While this is generally true for entanglement (it is indeed defined in terms of the mathematical expression of the state), some entangled states can exhibit correlations much stronger than those of non-entangled (separable) states. Let’s now go back to the physics.
After this mathematical detour, we return to Alice, Bob, and Charlie. Suppose that Charlie now decides to prepare pairs of spins in the entangled state $|\Psi\rangle_{AB} = (|\uparrow\rangle_A \otimes |\uparrow\rangle_B + |\downarrow\rangle_A \otimes |\downarrow\rangle_B) / \sqrt{2}$. At this point, we cannot explain in detail the physical process to do so; however, it should be noted that this requires the two spins to interact (which was not the case when Charlie was preparing the states $|\uparrow\rangle_A \otimes |\uparrow\rangle_B$). Now, if Alice and Bob receive spins $A$ and $B$, respectively, and measure them in the vertical direction, what are the expected outcomes? Well, using again the
third postulate of QP, we immediately see that they both either obtain outcome ``up'' or ``down'', and the two situations occur with probability $p = 1/2$. Again, as in the case in which Charlie was making use of the coin to prepare the two-spin state, we have perfect correlation in the vertical direction. But let us see what happens if Alice and Bob both measure in the horizontal direction. Using again that $|\uparrow\rangle = ( |\leftarrow\rangle + |\rightarrow\rangle ) / \sqrt{2}$ and similarly that $|\downarrow\rangle = ( |\rightarrow\rangle - |\leftarrow\rangle ) / \sqrt{2}$, we have
$$
\begin{aligned}
|\Psi\rangle_{AB} =& \frac{1}{\sqrt{2}} \left( |\uparrow\rangle_A \otimes |\uparrow\rangle_B + |\downarrow\rangle_A \otimes |\downarrow\rangle_B \right) \\
=& \frac{1}{2\sqrt{2}} \big[ (|\leftarrow\rangle_A + |\rightarrow\rangle_A ) \otimes (|\leftarrow\rangle_B + |\rightarrow\rangle_B) \\
&+ (|\rightarrow\rangle_A - |\leftarrow\rangle_A) \otimes (|\rightarrow\rangle_B - |\leftarrow\rangle_B) \big] \\
%=& \frac{1}{2\sqrt{2}} \big[ ( |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B + |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B) \\
%&+ ( |\leftarrow\rangle_A \otimes |\rightarrow\rangle_B - |\leftarrow\rangle_A \otimes |\rightarrow\rangle_B) \\
%&+ ( |\rightarrow\rangle_A \otimes |\leftarrow\rangle_B - |\rightarrow\rangle_A \otimes |\leftarrow\rangle_B) \\
%&+ ( |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B + |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B) \\
=& \frac{1}{\sqrt{2}} \left( |\leftarrow\rangle_A \otimes |\leftarrow\rangle_B + |\rightarrow\rangle_A \otimes |\rightarrow\rangle_B \right).
\end{aligned}
$$
From this last result, we can immediately see that their outcomes in the horizontal direction are also perfectly correlated! They both obtain the same result, “left” or “right”, with probability $p = 1/2$. This is the “extra" correlation (with respect to the coin-assisted preparation) that we were referring to initially. In fact, this is true for any direction they choose (as long as it is the same one for both). Interestingly, for this state, the two possible outcomes that can be obtained when either of the two spins is measured are always equally likely (hence unpredictable) and, yet, the two spins yield the same result.