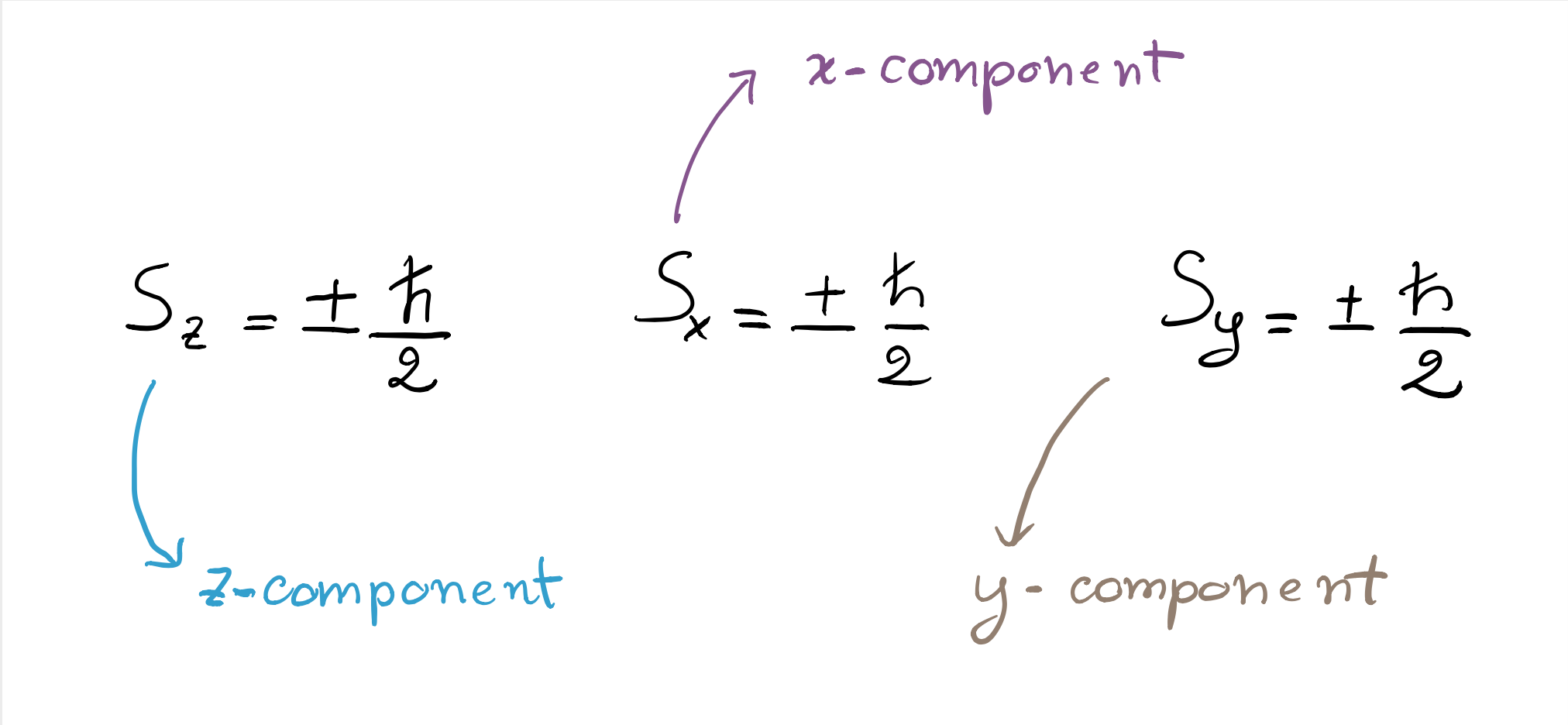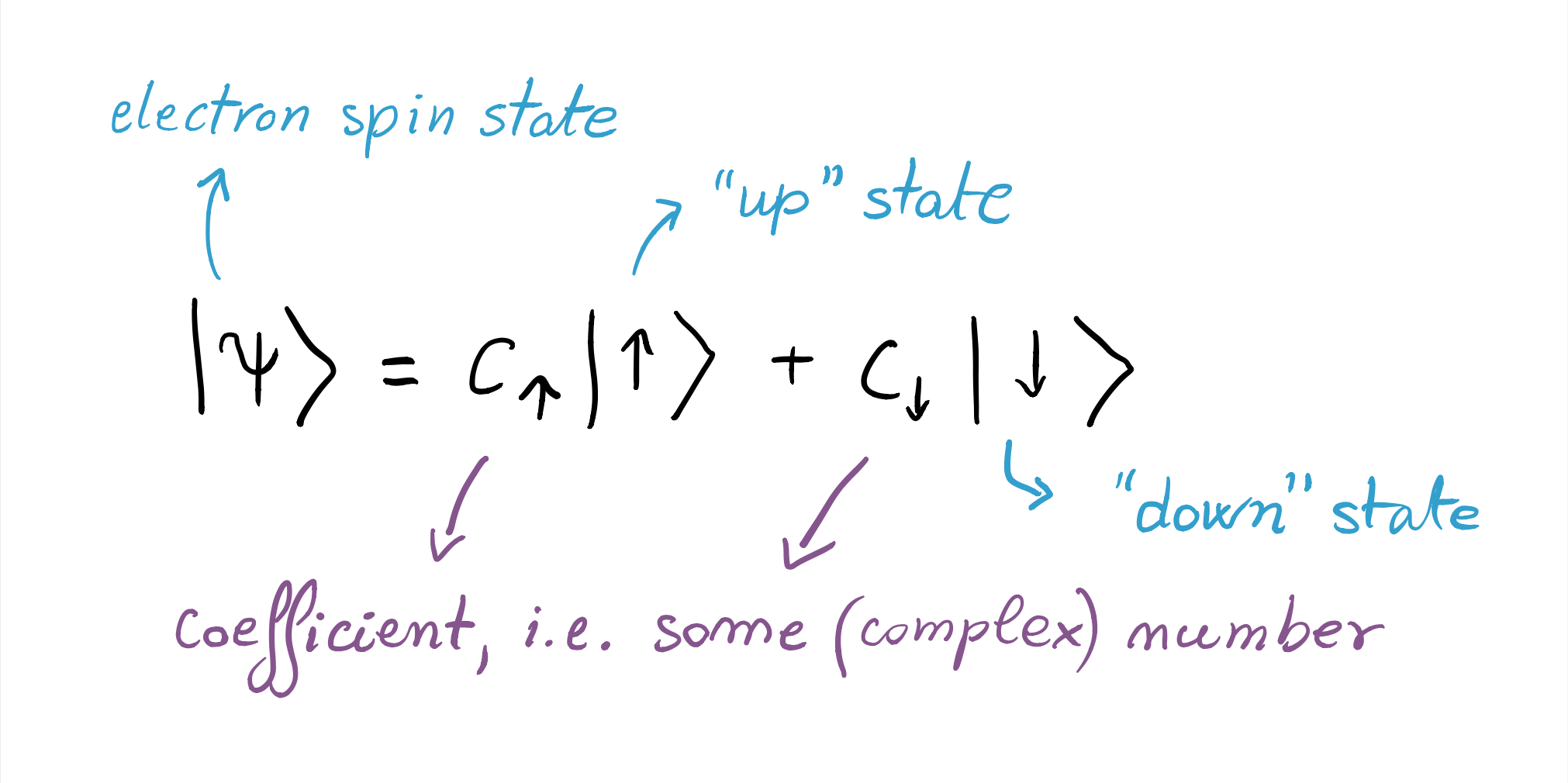QUEST
Quantum State
In this entry you will find information about what quantum physics is. Start from the section that feels easier or closer to you (play, discover, or learn), and then explore the others to see how your understanding shifts and expands!
"(the Stern-Gerlach) experiment illustrates in a dramatic manner the necessity for a radical departure from the concepts of Classical Mechanics”.
—
Jun J. Sakurai
Play
Quantum Playground is an art game that allows us to visualise key concepts of quantum physics, such as the quantum state, quantum superposition, interference, and the Schrödinger equation.
You can create a particle in a quantum superposition state by clicking or dragging your mouse across the Playground. As the quantum state begins to evolve, its pattern resembles a wave. At this point, click to perform a measurement and try to match the chosen node with the one where you think the particle will end up!
Credits:
Physicists: Guillermo García-Pérez, Sabrina Maniscalco, Laura Piispanen, Matteo Rossi, Boris Sokolov
Developer: MiTale
Discover
Perhaps the simplest and most versatile experiment to introduce the surprising behaviour of matter at the microscopic scale is the so-called Stern-Gerlach experiment. Quoting Jun J. Sakurai, “this experiment illustrates in a dramatic manner the necessity for a radical departure from the concepts of Classical Mechanics”. It was initially conceived in 1921 by Otto Stern, who realised it together with Walter Gerlach the year after at the Physics Institute of Frankfurt University. We will now describe this beautiful experiment and then ask ourselves the question: what can we learn about the quantum state of an electron from the experimental results?
According to the understanding of atomic physics in the early 20th century, it was believed that the motion of the electrons (negatively charged particles) around the nucleus (positively charged) could happen only at some fixed distances, called orbitals or energy levels, in a sort of scaled-down solar system. During their motion, the electrons would create a magnetic field conferring the atom a magnetic property called magnetic angular momentum or magnetic moment. In other words, the atom could be regarded as a tiny magnet, with its own north and south poles. In the early days of Quantum Mechanics (QM) the separation of the electrons in different orbits was named space quantisation, and in this context, Stern and Gerlach conceived their experiment with the purpose of testing such theoretical hypothesis for certain atoms.
Today we know that the angular momentum is composed of the sum of an orbital part, describing the electrons’ rotation around the nucleus, and an intrinsic part, called spin, that at variance with the former one, does not have a classical counterpart and can only take some fixed, i.e., quantised, values. Accidentally, Stern and Gerlach chose atoms with null orbital momentum; their angular momentum was exclusively given by the spin! That’s the reason why their experiment is often regarded as the first one demonstrating the existence of the electron’s spin. Nevertheless, such relevant result was only recognised a posteriori; the two physicists only wanted to prove the space quantisation of orbital momentum, that is, to verify the quantum variant of the atomic magnetism as opposed to the classical one. Apart from the original motivations and the historical scenario where the two German physicists acted, we’ll use the Stern-Gerlach experiment to illustrate some of the fundamental quantum concepts (and the inadequacy of the classical, i.e., non-quantum, ones), starting from the vectorial description of quantum states.
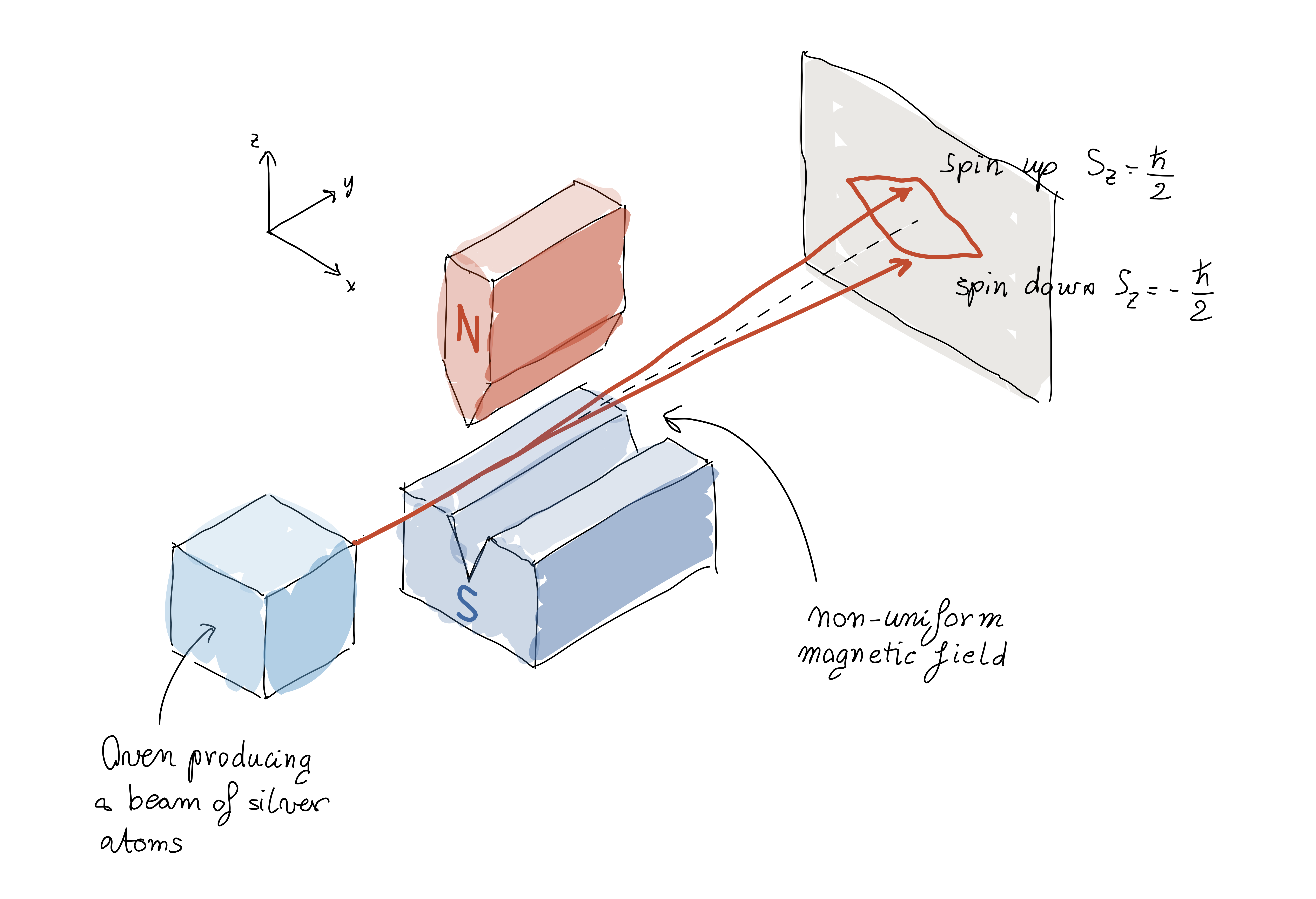
In the experiment silver atoms pass at high speed through a specially designed magnetic field, so that their trajectories deviate depending on the orientation of the north and south poles of the atom; the atoms later collide with a photographic plate, making the deviation, and hence the orientation of the magnetic moment causing it, visible. The setup is sketched and explained with more detail in the Figure below.
First, silver atoms are heated in an oven. The oven has a small hole through which some of the silver atoms escape. The beam is then subjected to an (inhomogeneous) magnetic field produced by a pair of pole pieces, one of which has a very sharp edge. Eventually the atoms meet a photographic plate, where they collide.
When an atom goes through the magnet, it’s pulled downwards or upwards, depending on the orientation of its magnetic moment. According to classical physics, one would expect to obtain a continuum of collisions on the photographic plate: if the atoms come out of the oven with any orientation, their trajectories will deflect by any angle between the extreme ones corresponding to the vertical orientations of the magnetic moment (in fact, due to thermal effects, the atoms do actually have randomly oriented magnetic moments; there isn’t a “preferred” orientation). However, the results showed otherwise, and only two outcomes were observed, as expected by quantum theory. The atoms either deviated upwards or downwards by some given angle, as if the vertical orientation of the north and south poles could only have two values.
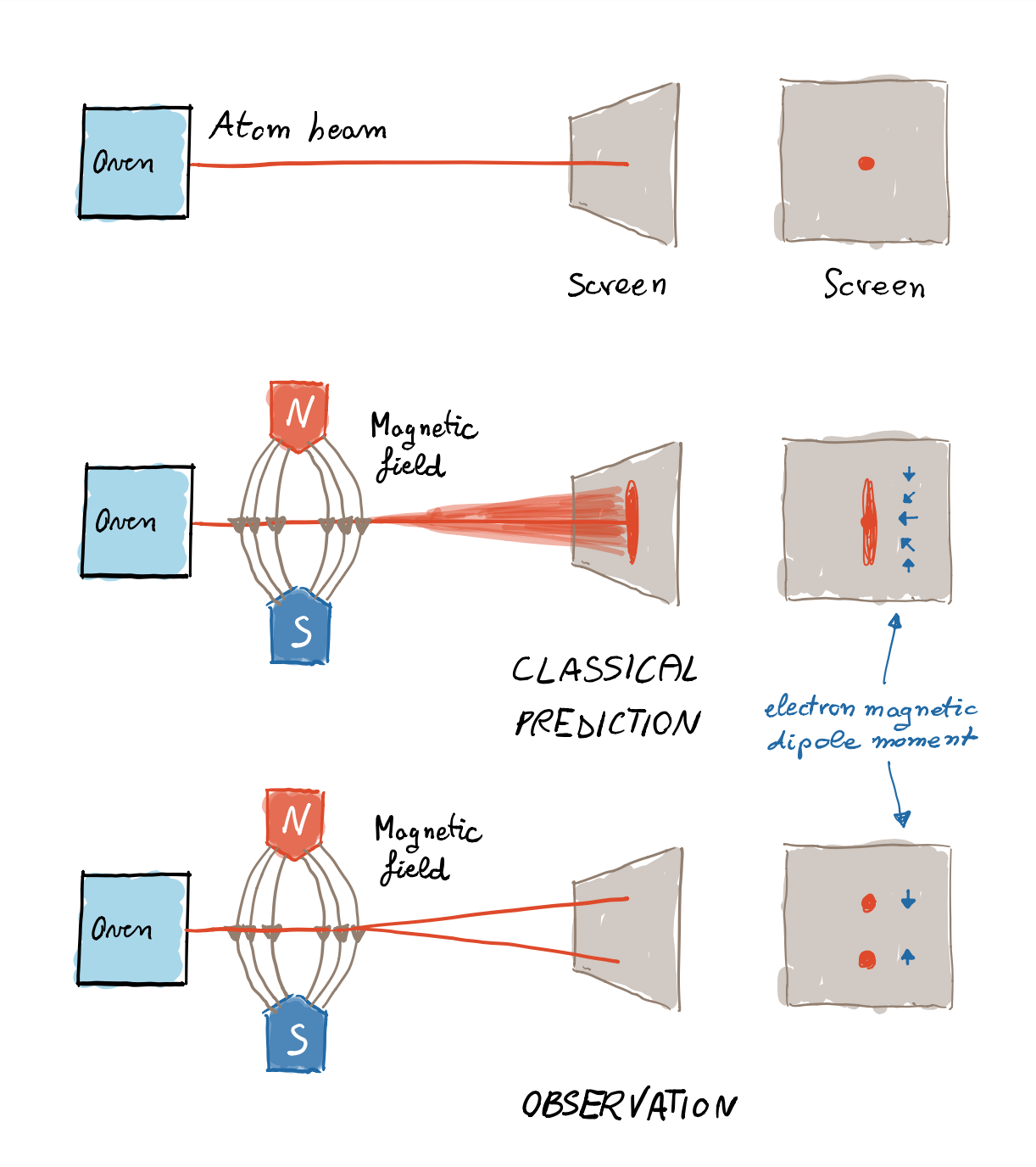
Expected experimental results. From top to bottom 1) if there’s no magnet, the image on the screen reproduces the little hole of the oven from which the atoms escape, because without a magnetic field the beam is not deflected; 2) expected results according to the classical hypothesis; 3) expected results according to the quantum hypothesis. Notice that the electron magnetic dipole moment has opposite sign with respect to the spin.
Therefore, the space quantisation was confirmed, even though the actual meaning of the results was fully understood few years later, only after the theoretical proposal of the electron’s intrinsic angular momentum, the spin, contributing to the magnetic moment. In particular, the magnetic moment of silver atoms is exclusively given by the spin of the electron in the most external orbital, and that’s why only two values, “up” and “down”, are observed. It was later discovered that electrons are particles with spin $1/2$, and that the two possible spin values in the vertical direction are multiples of some fundamental unit of angular momentum; it turns out that such values are $\pm \hbar/2$, where $\hbar$ is the so-called Planck constant (a fixed number).
Note that there is nothing special in the chosen vertical direction (i.e., the $z$-axis in the first figure); the quantisation of the outcomes is observed even if the experimental apparatus is rotated. For instance, if it is rotated by 90 degrees, the atoms deviate towards the left or towards the right (the $x$-axis in the figure), and only the outcomes “left” or “right” are registered on the plate. Indeed, since the electron´s spin is equal to $1/2$, it can only take two values in any direction, which means that the component of the spin along the $x$, $y$, or $z$ directions can only be
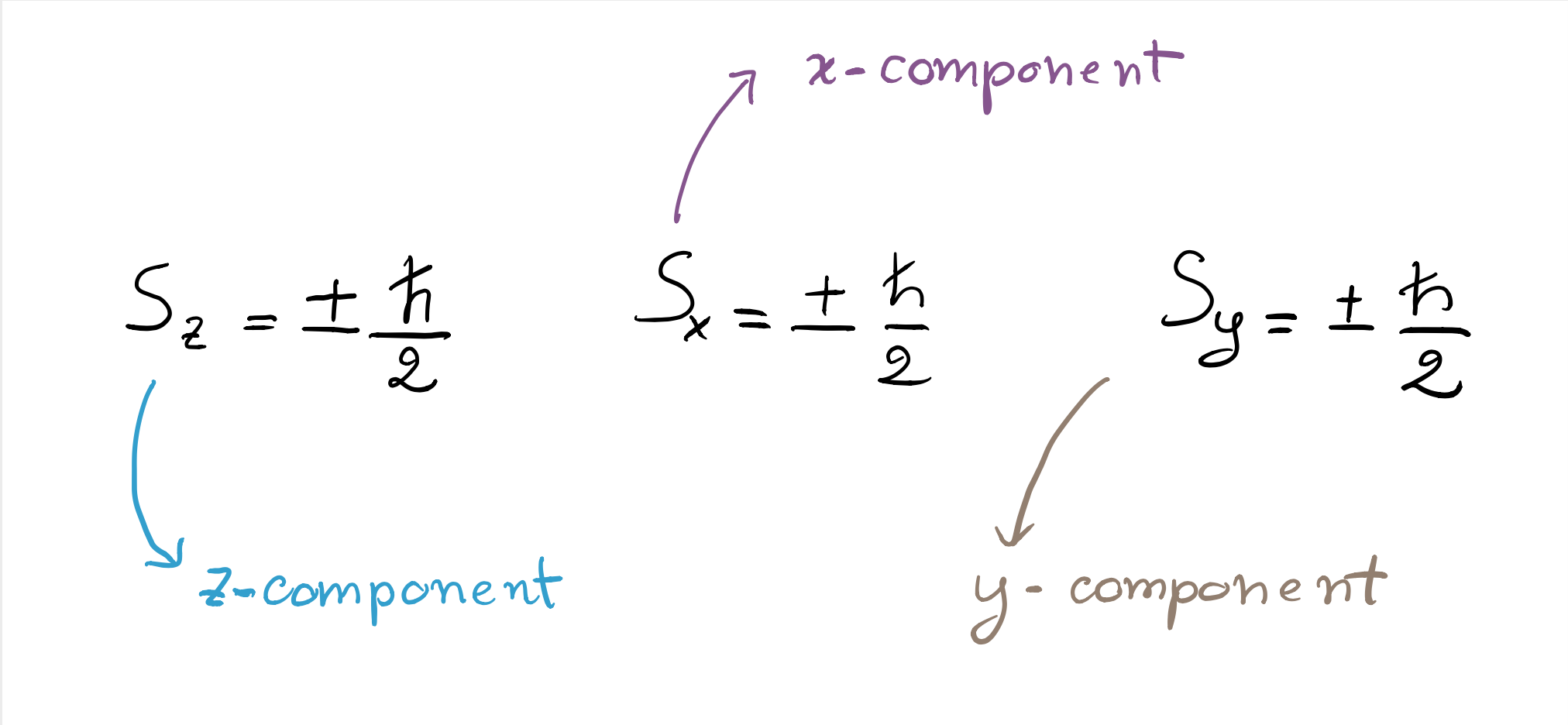
Beware! As we will see in the Heisenberg principle entry, at most one of them can have a well-defined value at any given time.
Now we may wonder, what is the state of the spin of a silver atom after it passes through the vertically oriented magnetic field? It would appear from the above experiment that it can only be “up” or “down”. However, as we will see in the entries on quantum superposition and wave-like behaviour, in a variant of this experimental setting, it is consistent with the observations to assert that it is in both at the same time. Mathematically, this is encoded in the first postulate of quantum theory, which tells us that the state of the electron can be represented as the vectorial sum
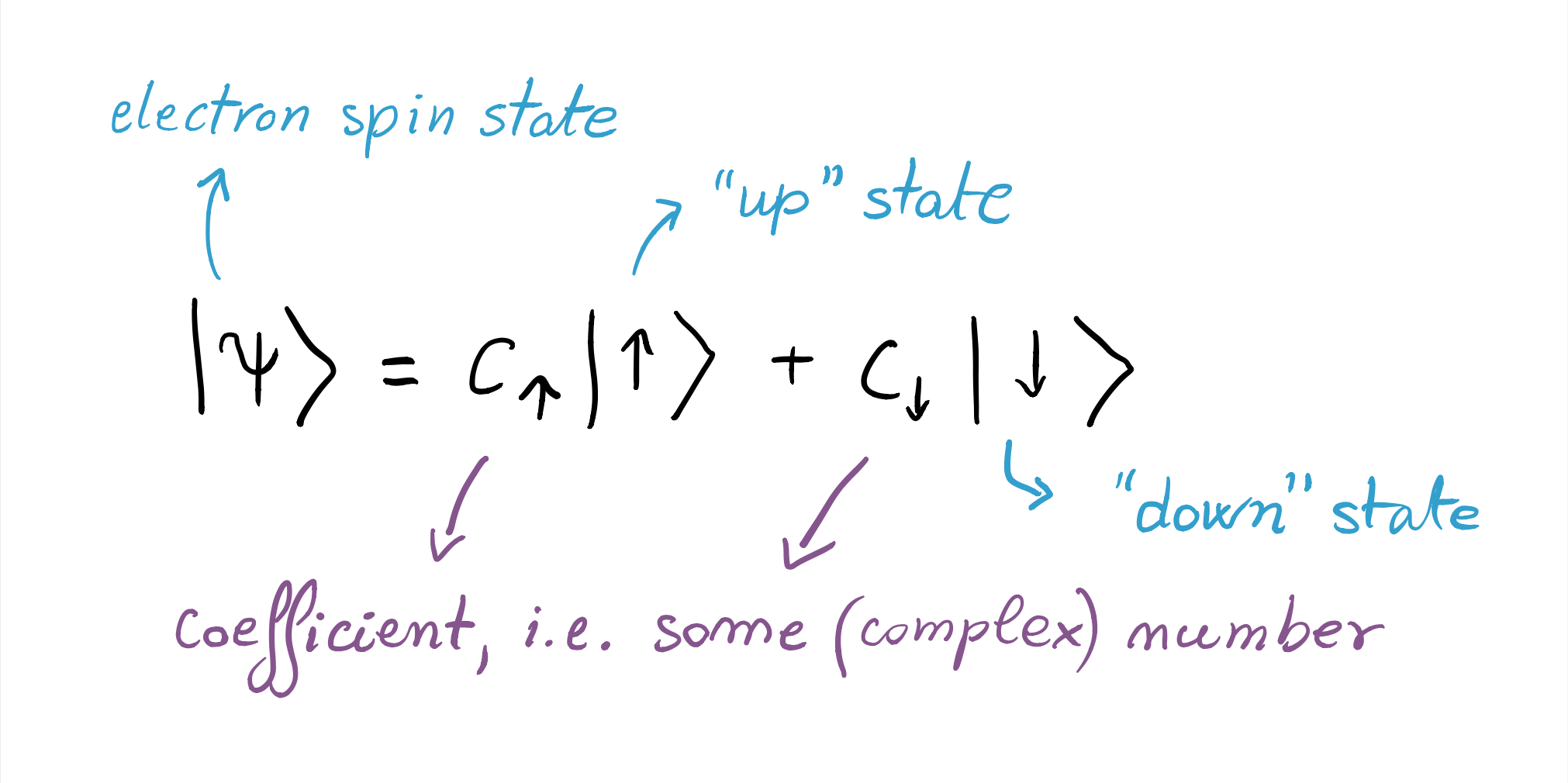
At this level, the fancy-looking brackets simply mean “the state of the system is what is written inside”. The use of such notation is consistent with the observation, on the photographic plate, of traces of the atoms in only two points, corresponding to the “up” and “down” states. Pay attention: this notation does not mean that the atoms are sometimes in the state “down”, sometimes in the state “up”. Jump to the superposition and measurement entries to discover why!
Learn
In this link you’ll find a short introduction to the mathematical description of the quantum state.
© QPlayLearn 2020-2024 | Design by Bitflow